
LOG関数は指定した数値を元に対数を求めるExcelの関数だ。数値と底を指定することで、対数を求められる。
目次
LOG関数をExcelで使う方法が分からない、という方もいるのではないだろうか。
本記事ではExcelでLOG関数を使う方法について解説する。また、常用対数のグラフを作成する方法についてもまとめた。
LOG関数とは?
LOG関数は、指定した数値を元に対数を求めるExcelの関数のことである。対数とは、ある数が別の数の何乗であるかを表現したものだ。
たとえば、LOG(8,2)の場合、8は2の何乗であるかを求めることになる。この場合、8は2の3乗なので答えは「3」となり、LOG関数は「3」を出力する。
■LOG関数の書式
LOG関数の書式は次のとおりである。
- =LOG(数値, [底])
1つめの引数に元にする数値、2つめの引数に底を指定する。
2つめの引数は省略も可能。省略した場合、底は自動的に「10」となる。
LOG関数の使い方
LOG関数の使い方についてここからみていこう。
次の2つの方法を順番に解説していく。
- LOG関数に底を指定する
- LOG関数の底を省略する
■1.LOG関数に底を指定する
LOG関数の第2引数に底を指定して実行する手順をまず解説しよう。
以下では「=LOG(8,2)」としている。これは、8は2の何乗であるかを求めようとしていることになる。
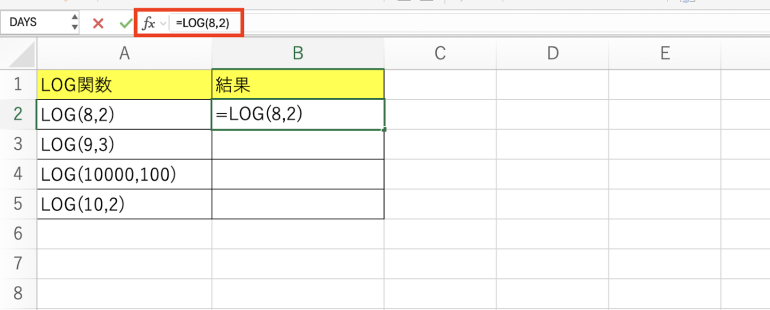
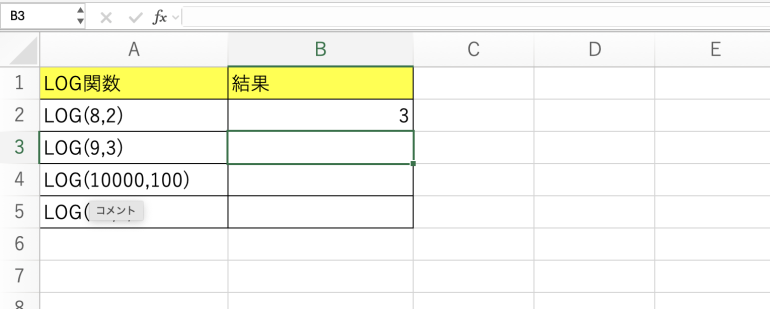
実行すると「3」と表示されている。8は2の3乗であるため「3」で合っていることになる。
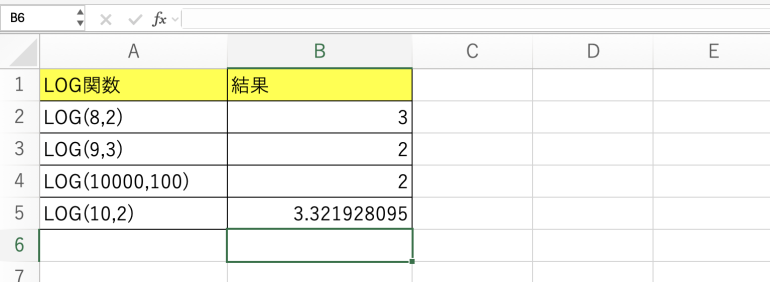
他の行も同じようにLOG関数を実行すると次のようになる。
9は3の2乗、10000は100の2乗なので、やはり合っていることになる。
また、10は2の3.321……も正しい結果となっている。LOG関数では小数点以下も表示される。
■2.LOG関数の底を省略する
続いて、LOG関数の2つめの引数を省略した例をみていこう。2つめの引数を省略した場合、底は自動的に「10」となる。
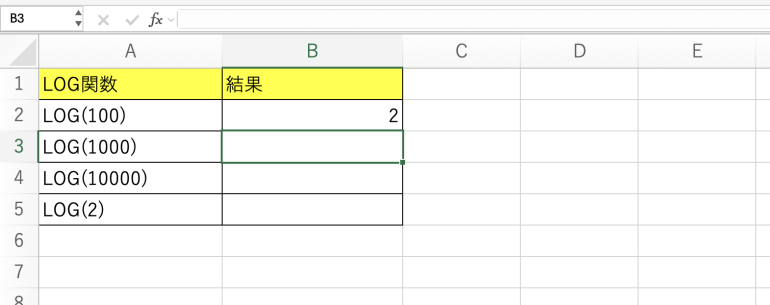
以下では「=LOG(100)」と記入している。これは、100は10の何乗であるかを求めようとしていることになる。
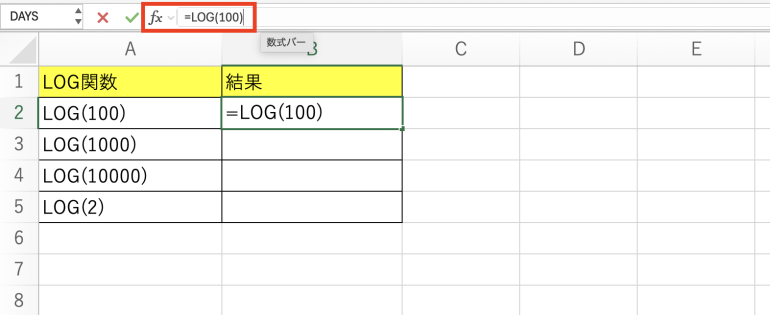
実行すると「2」と表示された。100は10の2乗であるため、合っていることになる。
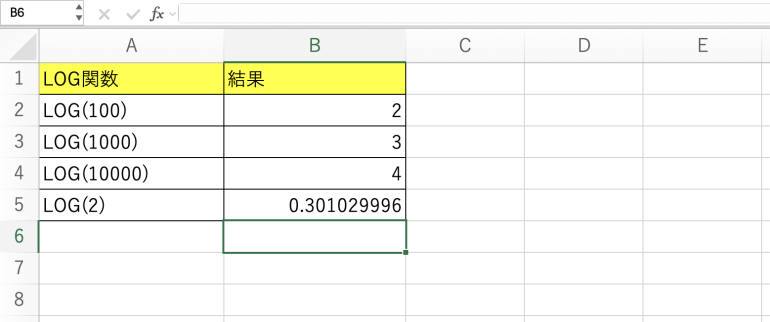
他の行でもLOG関数を使うと次のようになる。
1000は10の3乗、100000は10の4乗なので、やはり合っていることになる。
また、2は10の0.301……も正しい結果となっている。
LOG関数でグラフを作成する方法
LOG関数を使って常用対数のグラフを作成する方法を次に解説する。
手順は次のとおり。
- 数値の一覧を列挙する
- LOG関数で対数を求める
- グラフを作成する
- 近似曲線を追加する
ひとつひとつの手順について詳しくみていこう。
■1.数値の一覧を列挙する
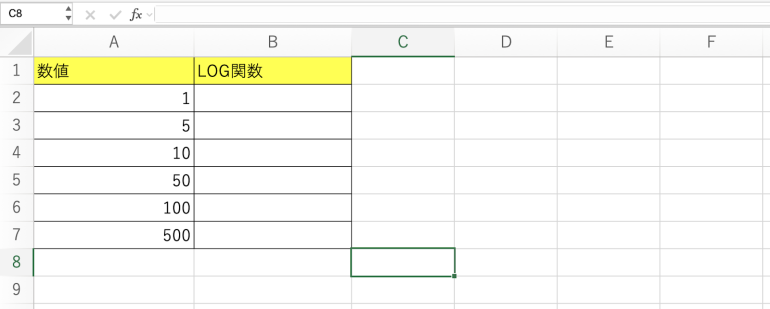
まず、対数を求めたい数値を表に列挙する必要がある。
以下の画像では「1、5、10、50、100、500」と記入している。
■2.LOG関数で対数を求める
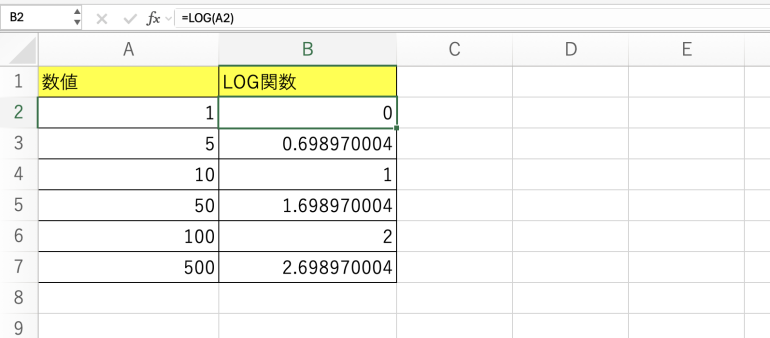
続いて、LOG関数で対数を求めていく。
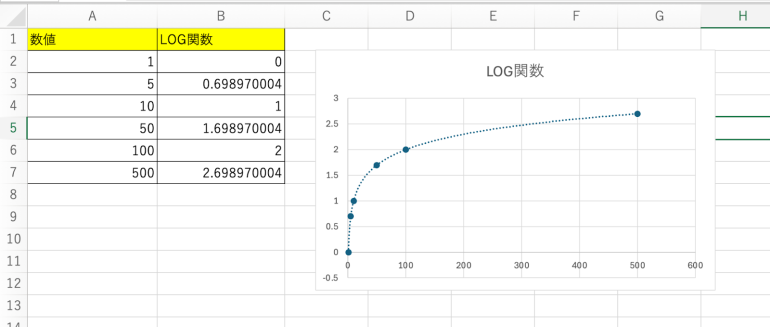
たとえば、B2には「=LOG(A2)」と記入する。1は10の0乗なので「0」と表示される。他の行にも同じように、LOG関数を使っていくと、次のような表が完成する。
■3.グラフを作成する
作成した表を元にグラフを作成しよう。
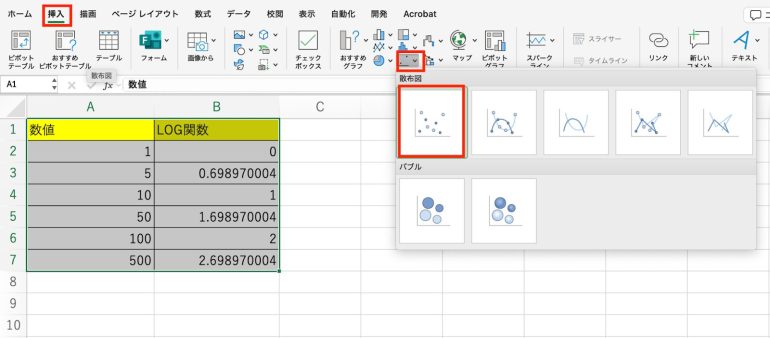
「挿入」タブから「散布図」をクリックする。散布図の一覧が表示されるが、ここでは1番最初の図をクリックして選択しよう。
すると、以下のように表を元に常用対数のグラフが表示されていることが分かる。
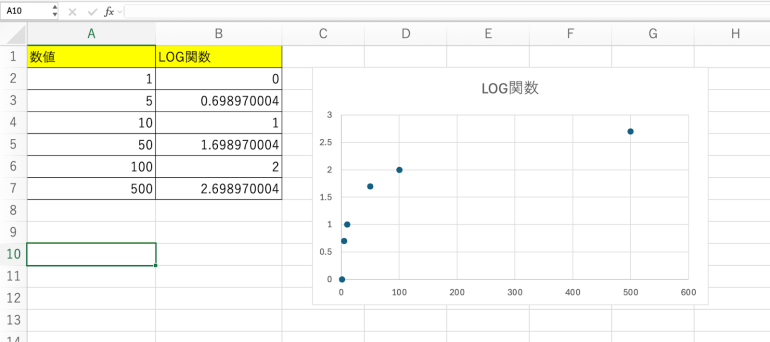
■4.近似曲線を追加する
更に、このグラフに近似曲線を追加しよう。
グラフを選択したら、「グラフのデザイン」というタブが表示されるのでクリックする。
「グラフ要素を追加」から「近似曲線」をクリックしよう。そこから「その他の近似曲線オプション」を選択する。
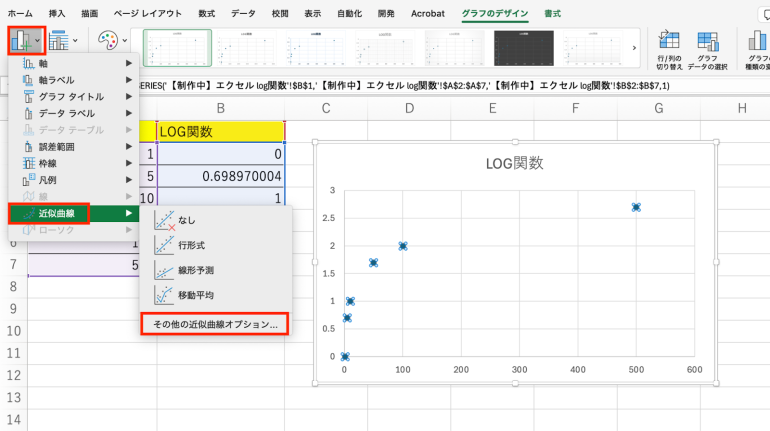
すると「近似曲線のオプション」が表示される。ここから「対数近似」にチェックを入れよう。
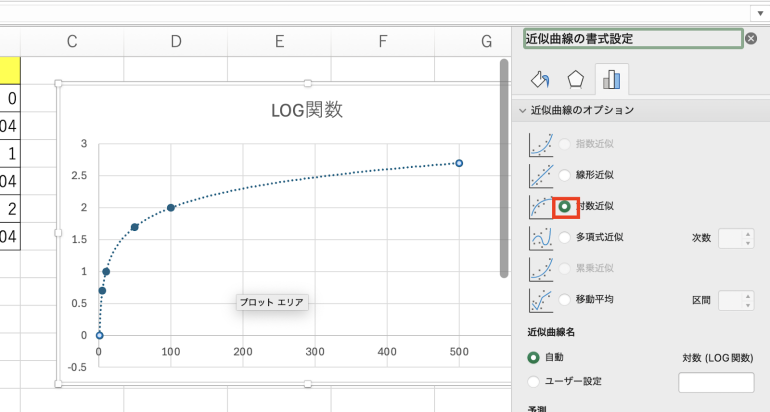
すると、常用対数のグラフに近似曲線が表示されていることが分かる。
まとめ
本記事ではExcelでLOG関数を使う方法について解説した。最後に、LOG関数の書式についておさらいしよう。
- =LOG(数値, [底])
具体的なLOG関数の使い方は次のとおり。
- LOG関数に底を指定する⇒例:「=LOG(8,2)」
- LOG関数の底を省略する⇒例:「=LOG(100)」
また、LOG関数でグラフを作成する手順は次のとおり。
- 数値の一覧を列挙する
- LOG関数で対数を求める
- グラフを作成する
- 「挿入」⇒「散布図」⇒1番最初のグラフをクリック
- 近似曲線を追加する
- グラフを選択
- 「グラフのデザイン」⇒「グラフ要素を追加」⇒「近似曲線」⇒「その他の近似曲線オプション」をクリック
- 「対数近似」にチェックを入れる
ExcelでLOG関数を使えば、対数を簡単に求めることができ、更にグラフ作成まで行える。
構成/編集部















 DIME MAGAZINE
DIME MAGAZINE













