Excelの回帰分析って何？熱い日ほどアイスが売れる理由など事件との関係性を調べる方法

回帰分析の活用事例

回帰分析は、予測や傾向の把握を目的に多くの分野で活用されている。ここでは、実際のサンプルデータを使って、ビジネスでの活用例を具体的に紹介する。

■広告費と売上

このデータをもとにエクセルで散布図を作成し、「近似曲線」を追加すると、回帰直線と回帰式が表示される。

ある企業が「月ごとの広告費」と「売上金額」の関係を調べたいと考えたとする。以下のようなデータをエクセルに入力した上で、回帰分析を行う。

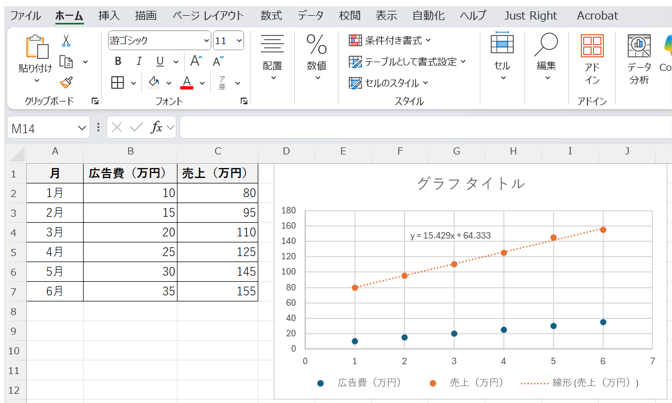
近似式が次のように表示されている

y = 15.429x + 64.333

この式の意味は以下の通りである。

x（広告費）が1万円増えるごとに、売上yが15.429万円増える傾向がある

広告費が0円のときでも、基礎的に売上は64.333万円あると予測される

まとめ

回帰分析は、日常やビジネス、学術の現場で広く使われている基本的な統計手法である。エクセルを使えば、関数や分析ツールを活用して誰でも簡単に回帰分析を行うことができる。重要なのは、結果を「どう読み取り、どう活かすか」である。本記事で紹介した内容をもとに、まずは身近なデータで回帰分析を試してみるとよいだろう。

本記事の内容を以下で簡単におさらいしておこう。

• 回帰分析とは
  • 変数同士の関係性を数式で表す分析手法。因果関係を見つけるのではなく、傾向を把握することが目的。
• 単回帰と重回帰：
  • 単回帰：1つの説明変数と目的変数の関係（例：気温とアイスの売上）
  • 重回帰：複数の説明変数を使って目的変数を予測（例：気温、湿度、日照時間と売上）
• 回帰直線の式：y = ax + b
  • a＝傾き、b＝切片、x＝説明変数、y＝予測される結果
• Excelでの実行手順：
  • データ入力（例：A列＝気温、B列＝売上）
  • 散布図作成（挿入 → 散布図）
  • グラフに「近似曲線」追加 → 数式表示をチェック
  • [ファイル] → [オプション] → [アドイン] → [分析ツール]を有効化
  • [データ] → [データ分析] → [回帰分析]を選び、X/Y範囲を設定して実行
• 関数での分析：
  • =SLOPE(売上, 気温) や =INTERCEPT(売上, 気温)
• 読み解きの注意点：
  • 決定係数（R²）が1に近いほど予測精度が高い
  • 相関と因果は別問題、外れ値には注意

関連記事：「Excelを使って相関係数を求める方法と注意点」

構成／編集部