
回帰分析とは、変数同士の関係性を数式で表す分析手法。傾向を把握することができる。エクセルで分析する場合は、散布図作成から近似曲線を引く方法と、SLOPE関数やINTERCEPT関数を用いる方法がある。
目次
「気温が上がるとアイスの売上は増えるのか」「広告費を増やせば売上は伸びるのか」といった、データどうしの関係性を分析するのに使えるのが「回帰分析」である。回帰分析は、統計学の基本的な手法の1つであり、エクセルを使えば誰でも簡単に実践できる。
本記事では、回帰分析の概要から、エクセルでの実行方法、活用事例までをわかりやすく紹介する。
回帰分析とは何か?
回帰分析は、2つ以上の変数の関係を明らかにするための分析手法だ。
■回帰分析の定義と目的
回帰分析とは、「ある変数が他の変数にどのように影響しているか」を数式で表す手法である。たとえば「気温が高い日ほどアイスの売上が増える」といった傾向があるとき、その関係性を分析するのが回帰分析の目的となる。
■単回帰分析と重回帰分析の違い
回帰分析にはいくつか種類があるが、基本となるのが「単回帰分析」と「重回帰分析」である。
単回帰分析は、1つの説明変数(原因)と1つの目的変数(結果)の関係を分析する方法である。例:「気温」と「アイスの売上」
重回帰分析は、複数の説明変数を用いて目的変数を予測する手法である。
例:「気温」「湿度」「日照時間」と「アイスの売上」
■回帰直線とその意味
単回帰分析では、次のような回帰式が得られる。
y = ax + b
- y:目的変数(売上など)
- x:説明変数(気温など)
- a:傾き(xが1変わるたびにyはどれだけ変わるか)
- b:切片(x=0のときのyの値)
この直線が「回帰直線」であり、データの傾向を数式で表現することができる。
エクセルで回帰分析を行う方法
エクセルを使えば、回帰分析は簡単に実行できる。以下に具体的な手順を示す。
■準備するデータ
まずは、分析に使うデータをエクセルに入力する。例として以下のようなデータを用意しよう。
A列:気温 B列:アイスの売上
■散布図を作る
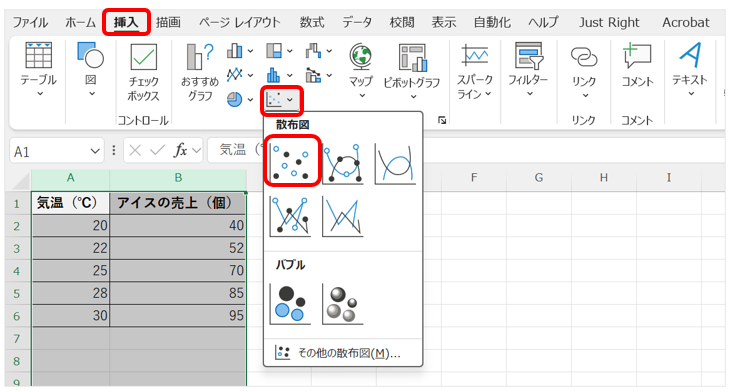
- A列:気温、B列:アイスの売上の2列を選択
- 「挿入」タブ → 「散布図」 → 「マーカーのみ」
点が並んだグラフが表示され、2つの変数の関連性を確認することができる
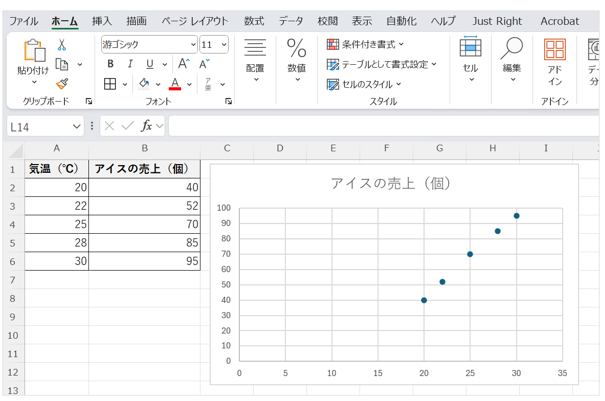
■近似曲線(回帰直線)を作成する
- +アイコン⇒散布図をクリック⇒ 近似曲線
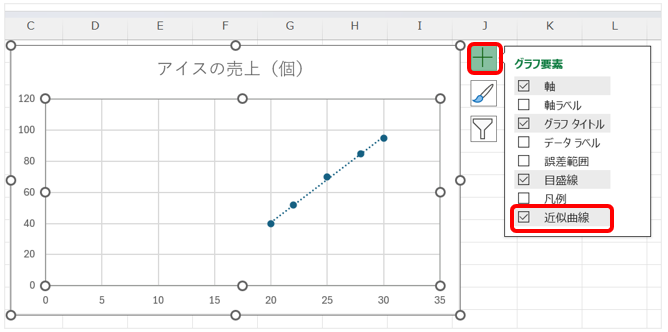
- 「数式をグラフに表示」をチェックする
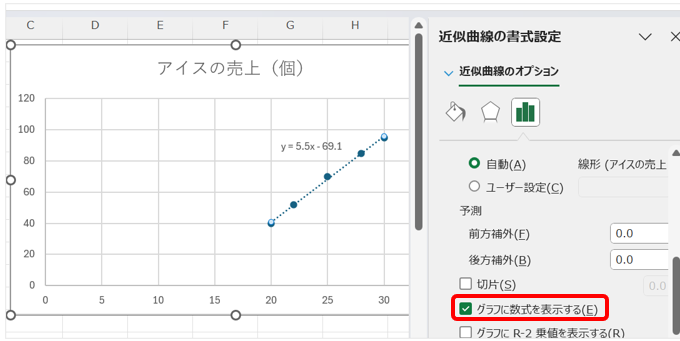
■分析ツールで回帰分析を行う
分析ツールを有効にする
- 「ファイル」→「オプション」→「アドイン」→「分析ツール」を有効
- データタブにデータ分析という項目が追加されるので、選択する
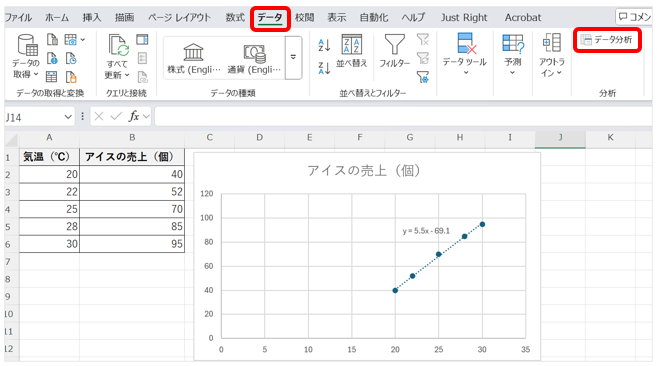
分析する
- 「データ分析」→「回帰分析」を選択
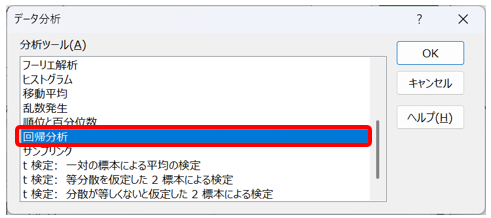
- 「Y入力範囲」に目的変数である売上、「X入力範囲」に説明変数である気温とする
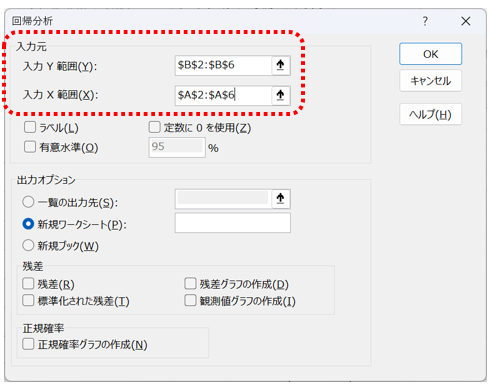
- それぞれの係数やp値、決定係数などの分析結果が別シートに出力される
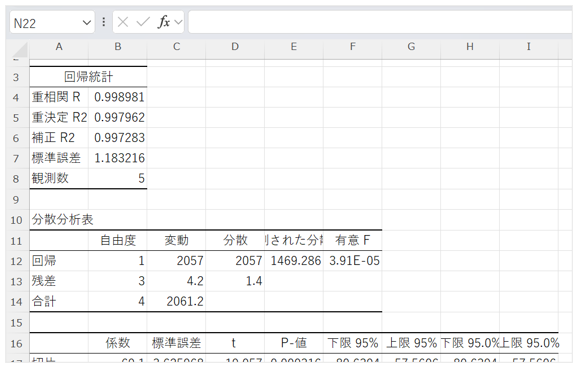
■SLOPE・INTERCEPT関数を使用
特に傾きや切片だけが欲しい場合に使用する。
- =SLOPE(売上列, 気温列) :傾きを求める
- =INTERCEPT(売上列, 気温列) :切片を求める
回帰分析の読み解き方と注意点
分析結果の見方と、誤った解釈を避けるための注意点を解説する。
■決定係数
決定係数(R²)は、回帰式がどれだけデータに当てはまっているかを表す指標である。1に近いほど精度が高く、0に近いと相関が弱いことを意味する。たとえばR² = 0.95であれば、「気温の変化が売上の変動を95%説明できている」ということになる。
■相関と因果
高い相関があったとしても、それが因果関係(原因と結果)であるとは限らない。たとえば「アイスの売上」と「日焼け止めの売上」が同時に増えても、片方がもう片方を引き起こしているとは限らない。
■外れ値の影響
一部に極端な数値(外れ値)があると、回帰直線が大きく歪んでしまう。分析前にはグラフでデータの分布を確認し、外れ値がある場合は取り扱いを検討すべきである。















 DIME MAGAZINE
DIME MAGAZINE













