
変動係数は、データのばらつきを平均値と比較して、安定性や信頼性を測るための指標。エクセルで計算する場合は、AVERAGE関数とSTDEV.P関数を用いる。構文は「=STDEV.P(範囲)/AVERAGE(範囲)」となる。
目次
統計学の学び始めに出てくる内容が「平均」や「標準偏差」だ。これらを使ってデータのばらつきを把握することができる。しかし、複数のデータを比較する際にはこの手法では限界がある。そんなときに便利なのが「変動係数」である。
本記事では、変動係数の意味やエクセルでの求め方、具体的な使い方を初心者にもわかりやすく解説する。
変動係数とは何か
変動係数とは、データのばらつきを相対的に示す統計指標であり、値の平均値に対して収集されたデータ点がどれくらい差があるのかを比率で表現できる。
ばらつきを測るには標準偏差がよく使われるが、平均値の違うデータ同士を比較する際には、それだけでは不十分な場合がある。変動係数を使えば、どれだけ平均値に対してばらつきがあるかを比率で把握することができ、異なるデータセットの比較が容易になる。
■変動係数の定義
変動係数とは、標準偏差を平均値で割った値である。計算式は次のとおり
変動係数(CV)= 標準偏差/平均
この式により、データのばらつきが平均値に対してどの程度大きいのかを把握できる。たとえば、標準偏差が100で平均が1,000の場合、変動係数は0.1となる。これはばらつきが平均値の10%であることを意味する。
■変動係数が重要な理由
例えば、ある商品Aの価格の標準偏差が100円、商品Bも100円だとする。しかし、商品Aの平均価格が1000円、商品Bの平均価格が500円だった場合、同じ100円のばらつきでもBのほうが変動が大きく感じられる。
このように、絶対的なばらつきだけでなく、平均に対する相対的なばらつきを把握する必要がある。変動係数は、異なる規模や単位をもつデータ間の比較において、とても有効な指標といえる。
変動係数の計算式と意味
ここでは、実際に式を見ながら変動係数の意味をより深く理解していこう。
■変動係数の計算式
Excelでの計算式は以下のようになる
=STDEV.P(範囲)/AVERAGE(範囲)
STDEV.Pは母集団の標準偏差を、AVERAGEは平均を求める関数である。
標本を使って計算する場合は STDEV.S() 関数を使用する。この違いは、データが全体の母集団を表しているか、一部の標本なのかによって選び分ける。
■変動係数の読み取り方
変動係数の数値が高いほど、ばらつきが大きいことを意味する。目安は以下の通り
ばらつきの数値
- 0.1以下:ばらつきが小さい(安定している)
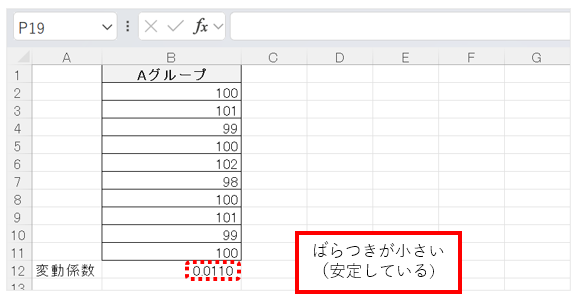
- 0.1〜0.3:中程度の分散
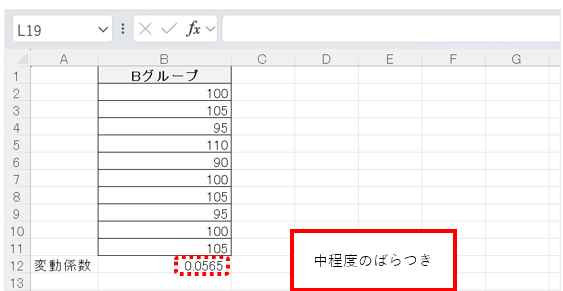
- 0.3以上:ばらつきが大きい(不安定)
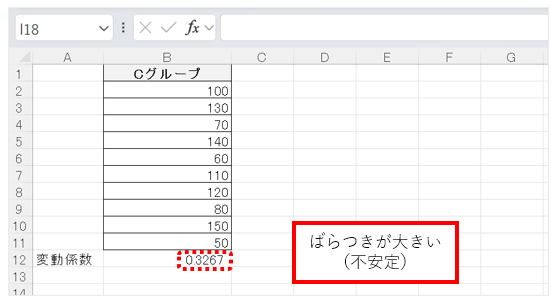
たとえば、試験の点数で変動係数が0.05であれば、受験者全体の点数が安定しているといえる。逆に0.4を超えるような場合は、学力差が大きいと判断できる。
エクセルで変動係数を求める方法
ここからは、エクセルを使って変動係数を求める手順を解説する。統計専用のソフトを使わなくても、Excelがあれば十分に分析可能である。
■使用する主な関数
変動係数をエクセルで算出する方法は、以下の2つの関数を用いる
=AVERAGE():範囲の平均値を出す
=STDEV.P()または=STDEV.S():標準偏差を算出する
■サンプルデータを使った具体例
以下のような売上データがあるとする
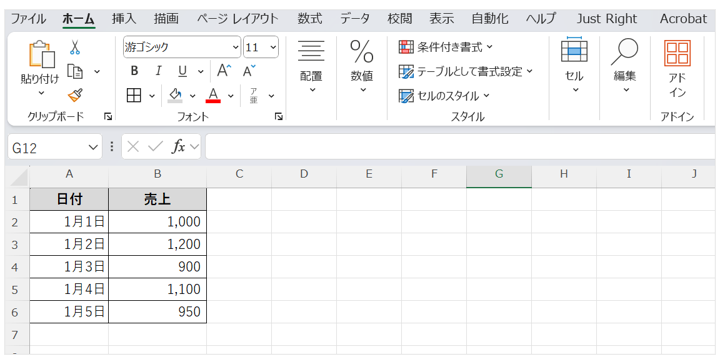
エクセルで売上データをA列とB列に入力した場合、B2:B6の範囲に対して次のように入力する
=STDEV.P(B2:B6)/AVERAGE(B2:B6)
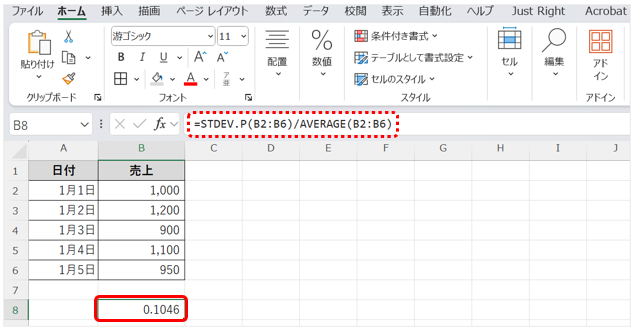
計算結果は約0.1046(10.5%)となる。これは、売上のばらつきが平均に対して10.5%であることを示しており、比較的安定しているといえる。
変動係数の使用例
変動係数は、様々な分野で活用されている。いくつかの使用例を紹介しよう。
■店舗ごとの売上のばらつき度を解析
店舗の売上の安定性を比較する場合、店舗ごとに規模が異なるため比較ができない。
変動係数をある程度の一般化ができる。
A店:CV≒0.12
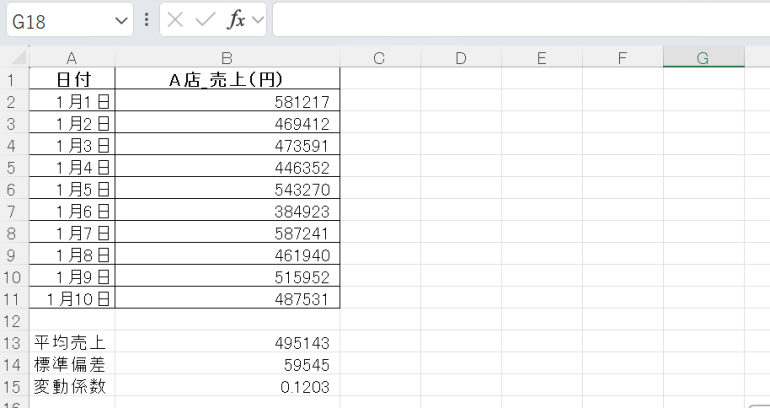
B店:CV = 4/30 ≒ 0.15
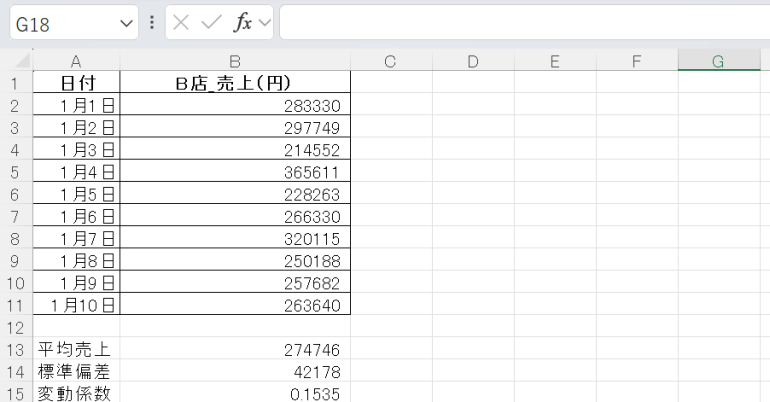
この場合、B店の方が変動係数が高く、売上のばらつきが大きい(=安定性が低い)と判断できる。
■実験データの信頼性を評価
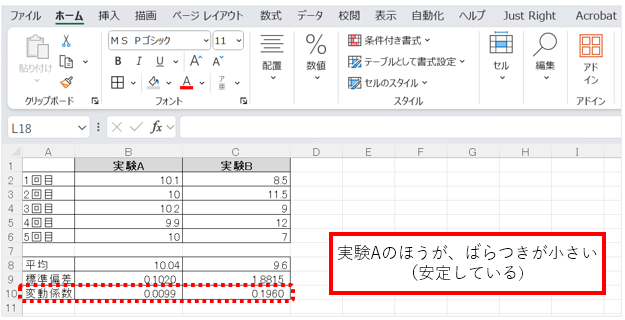
同じ条件で何度も実験を行った場合、変動係数が小さければ再現性は高いと考えられる。
たとえば、ある薬品の効果を調べるための実験で、同じ処理を5回行ったところ、効果量にばらつきが出たとする。変動係数を計算すれば、その再現性がどの程度か、数値で確認できる。















 DIME MAGAZINE
DIME MAGAZINE













