Excelのデータから「最小二乗法」を使って現象の関連性を分析する方法

データから特定の傾向を読み解く場面は、マーケティングや経済といった多岐にわたる分野でしばしば見受けられる。そのような状況下で、ある変数（X）が増加するにつれて、もう一つの変数（Y）がどのように変化するのか。この関係性を数式として表現する際、一般的に用いられる代表的な手法が「最小二乗法」だ。Excelの関数やグラフ機能を活用すれば、比較的容易にこの分析を扱うことができる。

本記事では、最小二乗法の基本的な考え方から、Excelでの具体的な活用方法に至るまでを、順を追って解説する。

最小二乗法とは

例えば、「気温が上がれば、アイスクリームの売れ行きが伸びる」といった現象について考えてみよう。

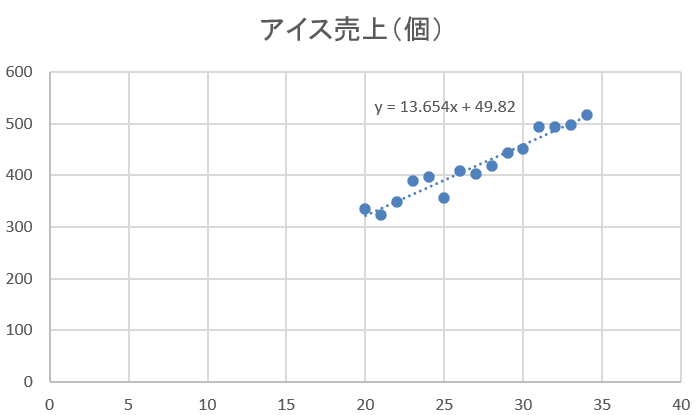
このように、気温と売上には、どうやら何らかの関連性があるらしいことがわかる。

最小二乗法は、まさにこの「X（気温）」と「Y（売上）」の関係性を、一本の直線で最も適切に描写するための数学的手法だ。この直線の式は Y=aX+b という形で表現され、a は直線の傾きを、b はY軸との切片を、それぞれ指し示す。

この直線を用いることで、例えば「気温が33℃だった場合、アイスは一体いくつ売れるのか？」といった具合に、具体的な販売数を予測できるようになる。

最小二乗法は、多数の点とそれらから引かれる直線との誤差を可能な限り小さくし、最も合う線を見つけ出す、とイメージすると分かりやすいだろう。

エクセルで最小二乗法を使う3つの方法

エクセルで最小二乗法を使うには下記の３つの方法がある。それぞれ解説しよう。

■方法１． SLOPE関数とINTERCEPT関数を使う

エクセルには、傾きと切片をそれぞれ求める関数がある。

傾きを求める：　=SLOPE(Yの範囲, Xの範囲)

切片を求める：　=INTERCEPT(Yの範囲, Xの範囲)

たとえば、YがB列、XがA列にある場合、以下のように入力する。

=SLOPE(B2:B6, A2:A6)

=INTERCEPT(B2:B6, A2:A6)

これで「Y = aX + b」のaとbが得られ、予測式が完成する。

■方法２．散布図＋近似直線を使う

視覚的に関係を確認するには、グラフの活用が便利である。

これで、回帰直線とともに数式（傾きと切片）が表示される。

■方法３．LINEST関数で詳細な分析をする

より詳しく分析したい場合は、LINEST関数が便利である。

構文：

=LINEST(Yの範囲, Xの範囲, TRUE, TRUE)

この関数は、傾き、切片だけでなく、決定係数や標準誤差なども返してくれる。

気温と売上のデータで分析を実践

実際のデータを使って分析してみるのが一番分かりやすい。ここでは、気温とアイスクリームの売上に関するデータを用い、その関連性を詳しく分析していこう。

■ステップ1：データを入力

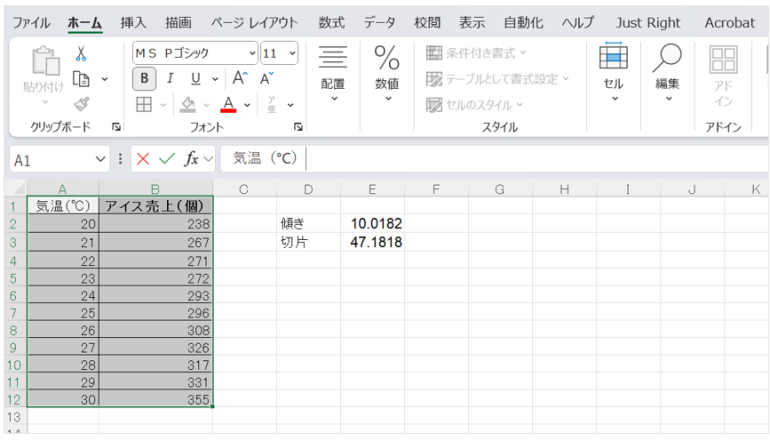
まずは、気温とアイスの売上に関するデータを準備し、シートに入力する。

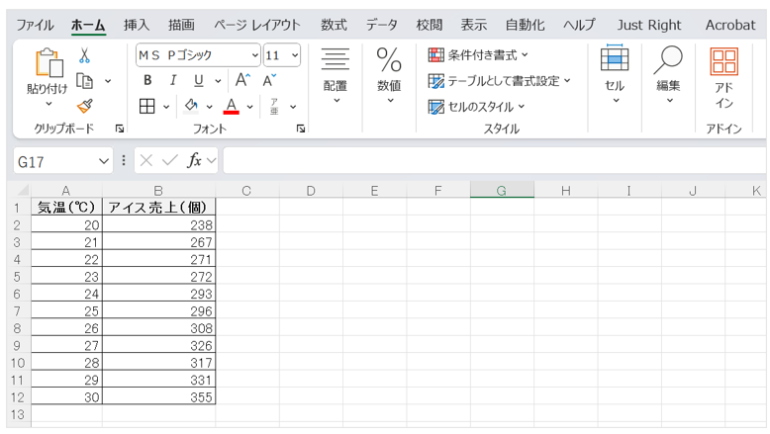
■ステップ2：関数で傾きと切片を出す

次に、以下の関数をシートに入力し、結果を確認することで、回帰直線の傾きと切片を算出する。

=SLOPE(B2:B12, A2:A12)

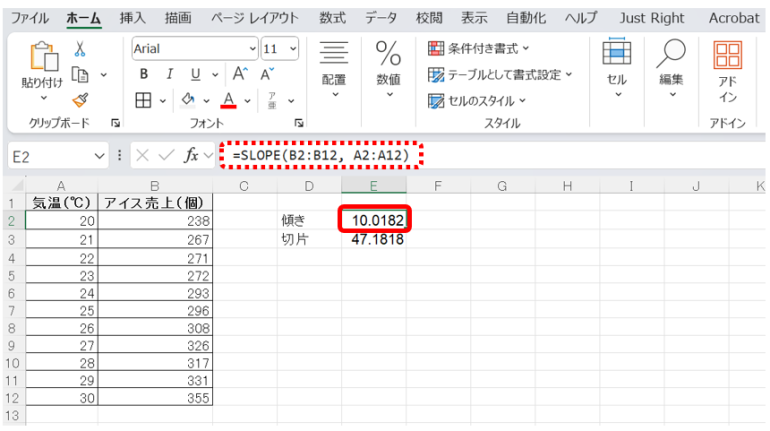
=INTERCEPT(B2:B12, A2:A12)

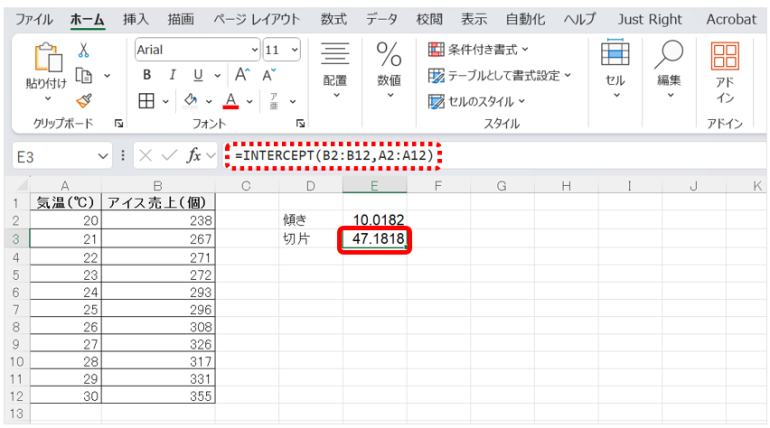
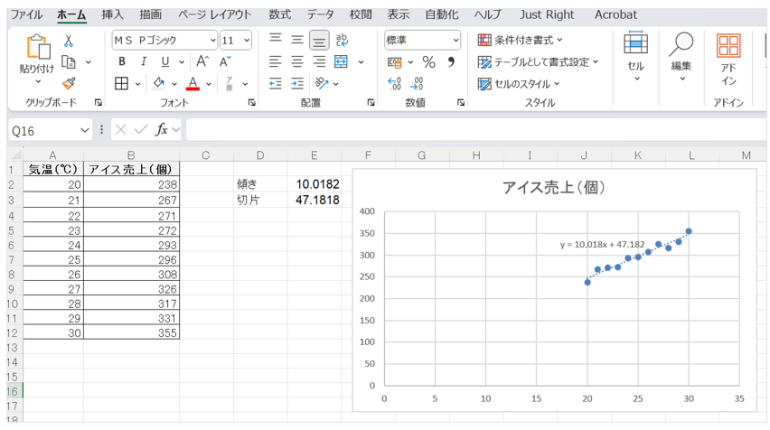
例えば、仮に結果として傾きが10、切片が47という値が出たとすれば、その予測式は「売上 = 10× 気温 +47」として表現されることになる。

■ステップ3：散布図を作成して確認

最後に、以下の手順で散布図を作成し、算出された回帰直線がデータにどの程度適合しているかを確認する。

1．分析対象のデータを選択する。

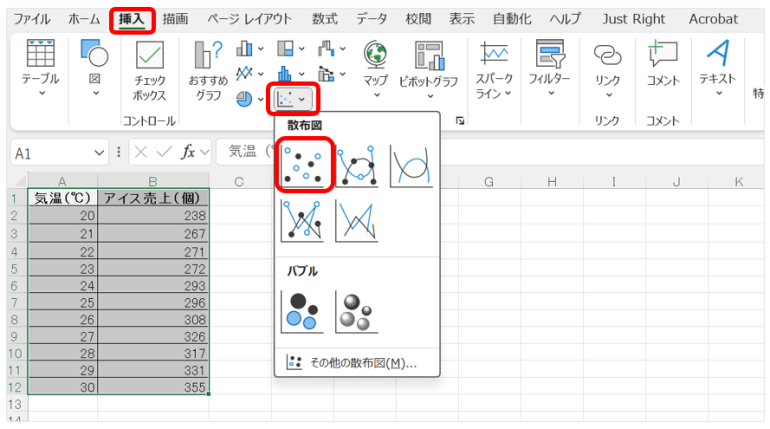
2．Excelの挿入タブから「散布図」を選び、グラフを作成する。

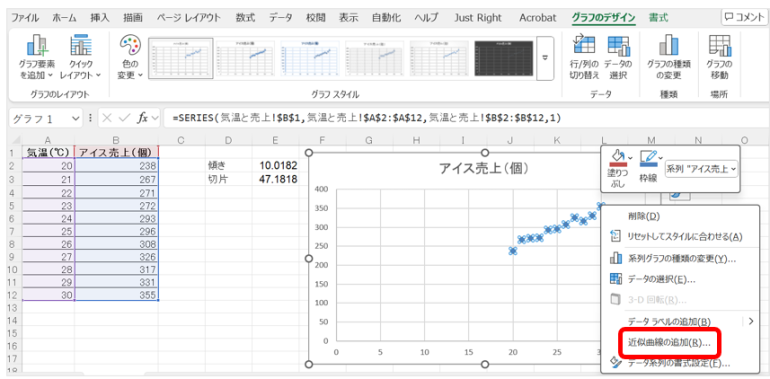
3．作成されたグラフ内で近似曲線を追加する。プロットした箇所を右クリックし「近似曲線の追加」をクリックする。

4．「線形近似」と「グラフに数式を表示する」にチェックを入れる。

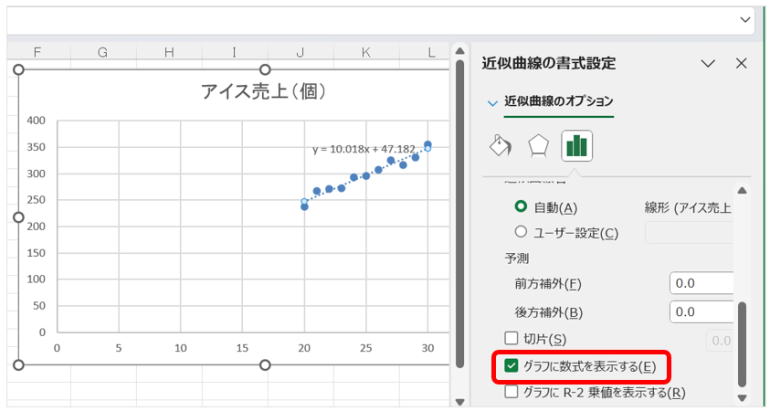
5．表示された数式が、先に関数で得られた結果と一致するかどうかを確かめる。

最小二乗法でわかること

最小二乗法は、データの傾向を読み解き、それに基づいて将来を予測する上で非常に役立つ手法だ。それぞれ具体的に解説しよう。

■傾向の把握

この手法により、データの背後に隠された傾向を数式として明確に表現できる。例えば、「気温が高いほどアイスクリームの売上が増加する」といった、複数の変数間における関係性を視覚的に捉えられるようになる。

■将来の予測

導き出された回帰直線の式を活用すれば、まだ観測されていないXの値に対し、対応するYの値を予測することが可能となる。これは、マーケティング分析や経済学における将来予測など、多岐にわたる分野で実際に活用されている。