DIME MAGAZINE
よくある質問
標準偏差に関してよくある質問と回答をあげて解説しよう。
■Q: 平均だけではダメなのか？
平均はデータ全体の傾向を把握するのに役立つが、ばらつき具合を知るには不十分だ。標準偏差を使うことで、データが平均値の周りにどれだけ散らばっているかがわかる。
■Q: 標準偏差が小さい場合、大きい場合の違いは？
標準偏差が小さい場合は、データが安定しており、一貫性が高いといえる。例えば、テスト点数がほとんど70点付近に集中しているようなケースだ。
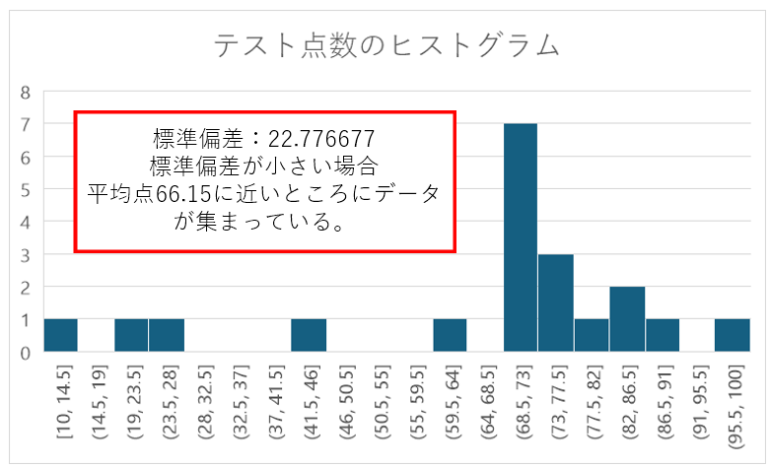
標準偏差が大きい場合は、データにばらつきがあり一貫性が低いということだ。データそれぞれの数値がまとまっていないことを表している。
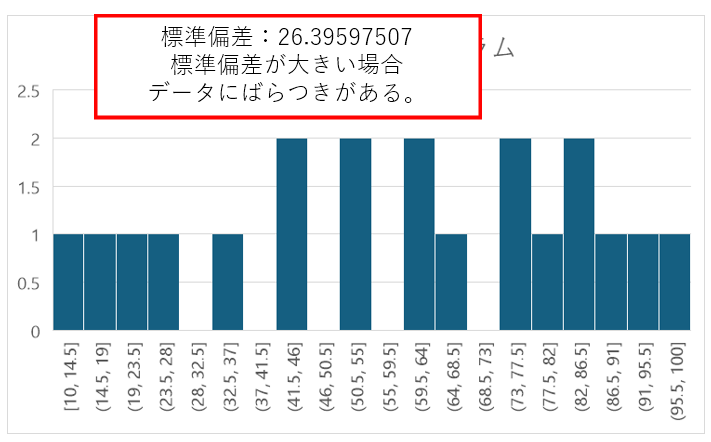
まとめ
標準偏差は、データのばらつきを数値で表す重要な統計値だ。エクセルを使えば簡単に計算できるので、日常のデータ分析にも応用できる。ヒストグラムと組み合わせることで、データの傾向を視覚的に把握することも可能だ。標準偏差を活用して、より深いデータの理解を目指そう。
本記事の内容を以下で簡単におさらいしておこう。
〇標準偏差とは
・定義: データが平均値からどれだけ離れているかを示す指標。
・平均との関係:平均はデータの中心を示すが、標準偏差はばらつきを測定。
〇エクセルを使った標準偏差の計算
＜使用する関数＞
・STDEV.P: データが母集団（全データ）である場合。
・STDEV.S: データが標本（一部データ）である場合。
＜計算手順＞
STDEV.Pを使用:
・データを入力（例: セルA1:A10に点数を入力）。
・計算セルに「=STDEV.P(A1:A10)」と入力。
STDEV.Sを使用:
・標本データを入力（例: セルB1:B5に一部データを入力）。
・計算セルに「=STDEV.S(B1:B5)」と入力。
〇ヒストグラムを用いたデータ分析
・目的: データ分布を視覚的に確認。
〇標準偏差とヒストグラムの関係:
・標準偏差が小さい: 平均周辺にデータが集中。
・標準偏差が大きい: データが広範囲に分布。
＜作成手順＞
・データ範囲を選択: 分析対象のデータを選ぶ。
・ヒストグラムを挿入:「挿入」タブ > 「ヒストグラム」を選択。
〇よくある質問
・平均だけではダメ？：平均は全体の傾向を示すが、ばらつきを把握するには標準偏差が必要。
・標準偏差の大小の違いは？：
小さい場合: データが平均付近に集中、一貫性が高い。大きい場合: データにばらつきがあり、一貫性が低い。
構成／編集部
最新号
