超かんたん！Excelで標準偏差を計算する方法

データ分析で標準偏差は重要な指標の一つであり、データの散らばり具合を表している。標準偏差は、統計値の一つであり、データ分析や計算の基礎となる。

この記事では、標準偏差の基礎知識とエクセルを使った計算方法をわかりやすく解説する。

標準偏差とは

まずは、標準偏差とはどのようなものか理解するために、標準偏差の定義と平均との関係を見ていこう。

■標準偏差の定義

標準偏差は、データが平均値からどれくらい離れているかを数値化したものだ。例えば、テストの点数を考えた場合、点数がみんな同じような点数であるほど標準偏差は小さくなる。一方、点数にバラツキがある場合は標準偏差が大きくなる。

■平均との関係

標準偏差は平均値を基準として計算される。平均値はデータ全体の中心を示しているが、それだけではデータのばらつきを知ることはできない。

例えば、あるクラスの数学のテストで平均点が70点だったとする。しかし、標準偏差が大きい場合、90点や50点の生徒が多い可能性があり、データの分布が広がっていることがわかる。

エクセルを使った標準偏差の出し方

エクセルを使って標準偏差を簡単に出すことができる。ここでは、標準偏差を計算する2つの関数と計算手順を紹介する。

■エクセルの標準偏差に関する2つの関数

エクセルでは、標準偏差を計算するために「STDEV.P」と「STDEV.S」という2つの関数が使える。

STDEV.P：データがすべて揃っている場合（母集団）に使う。

STDEV.S：データの一部を使って計算する場合（標本）に使う。

データ数が膨大な場合は、全てのデータを使って計算せず、一部の標本データを無作為に取り出して計算する場合がある。その場合は、STDEV.Sを用いて計算すると良い。

■STDEV.Pを用いた計算手順

データを入力：エクセルに標準偏差を計算したいデータを入力する。

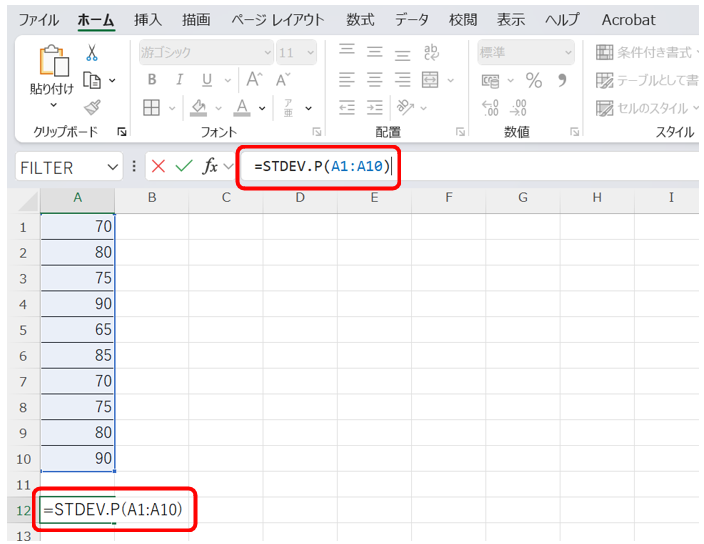
例：セルA1:A10にテスト点数（例：70, 80, 75, 90, 65, 85, 70, 75, 80, 90）を入力。

関数を入力：空のセルを選択し、「=STDEV.P(A1:A10)」と入力。

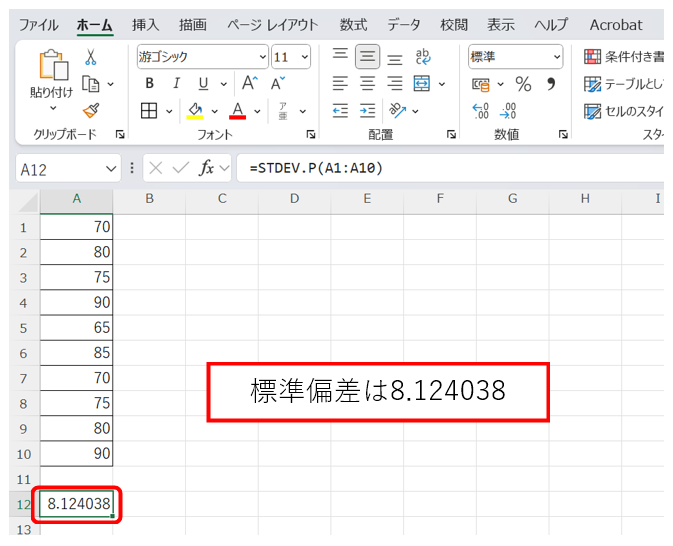
結果を確認：Enterキーを押して結果を確認する。

■STDEV.Sを用いた計算手順

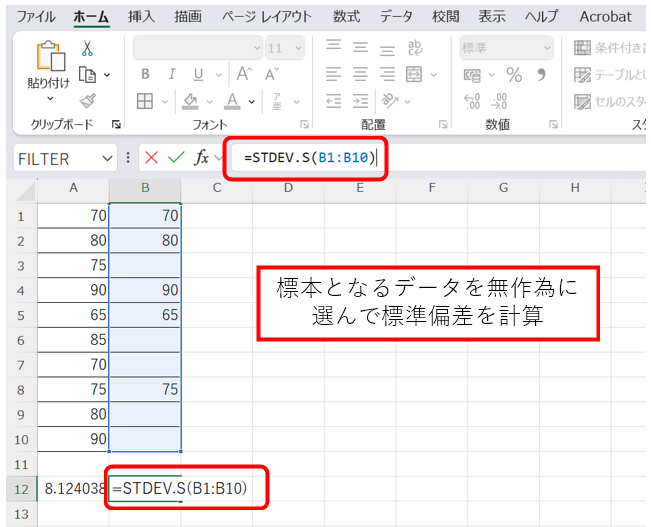
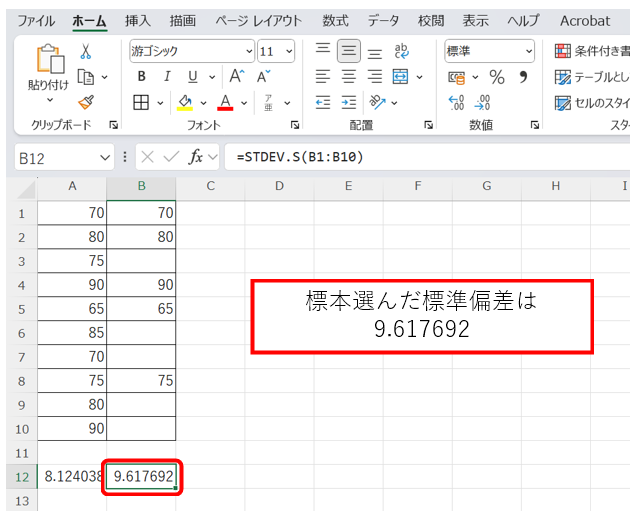
標本データを選択し、セルB1:B10に標本データを入力する。

関数を入力：空のセルを選択し、「=STDEV.S(B1:B10)」と入力。

結果を確認：Enterキーを押して結果を確認する。

標準偏差を活用したデータ分析の例

標準偏差を活用したデータ分析でデータのばらつき状況が確認できる。ヒストグラムはその代表的な手法だ。

■ヒストグラムを用いた分析方法とは

ヒストグラムは、データの分布を視覚的に理解するためのグラフだ。データがどのように分布しているかを一目で確認できるため、標準偏差と組み合わせて使うと便利だ。

例えば、テスト点数がどの範囲に集中しているかを確認する際などに役立つ。

■ヒストグラムの作成手順

ヒストグラムの作成手順は以下のとおりだ。

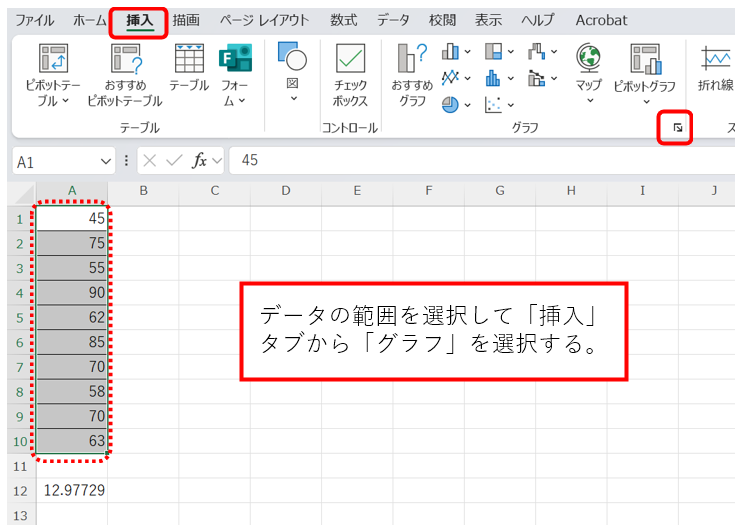
手順1．データ範囲を選択：分析したいデータを選択する。

手順2．ヒストグラムの挿入：「挿入」タブをクリックし、「グラフ」を選択する。

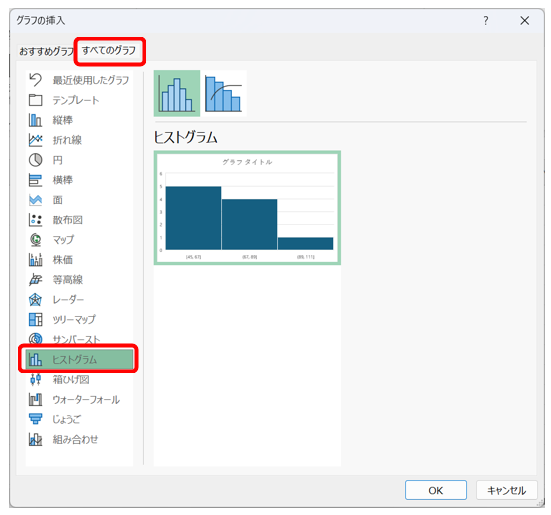
手順3．「すべてのグラフ」から「ヒストグラム」を選択する。

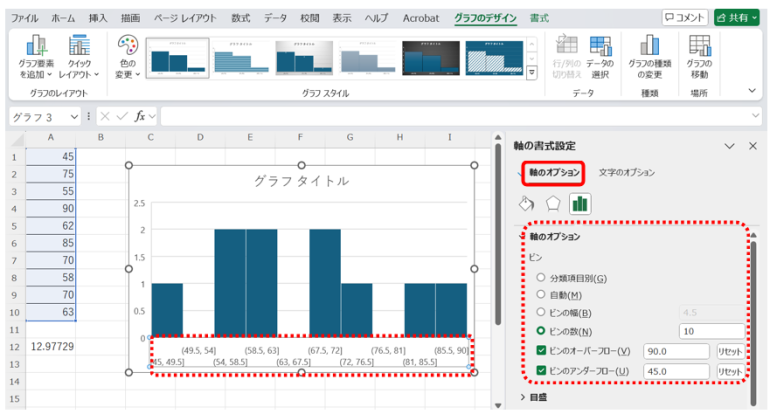
手順4．グラフの横軸を選択して「軸のオプション」を表示し、ピンの幅やピンの数、ピンのオーバーフロー・アンダーフローなどを設定し、見やすく調整する。

手順5．見た目の調整：グラフの色やタイトルなどをつけて仕上げる。

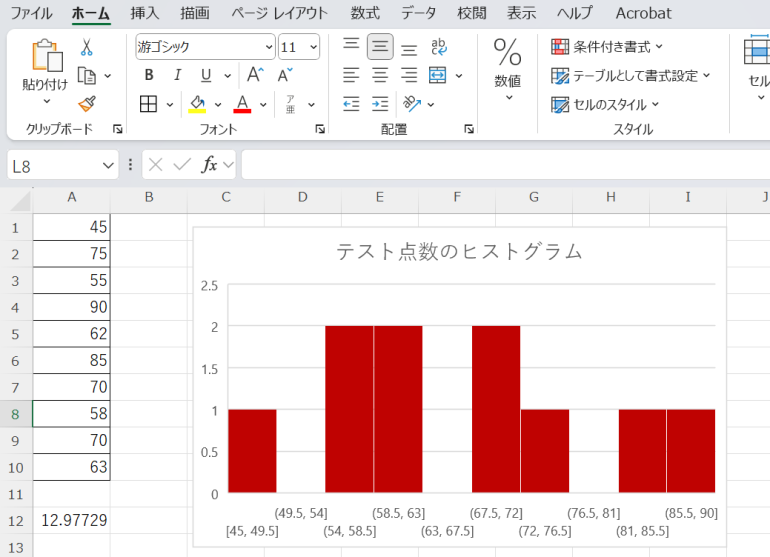
点数を10点刻みに分けてヒストグラムを作成することで、どの点数帯に集中しているかがわかりやすくなる。

■ヒストグラムの分析例

標準偏差が小さい場合：データが平均値周辺に集中している。

標準偏差が大きい場合：データが平均値から大きく離れている。

例：テスト点数が50点から90点まで幅広く分布している。

ヒストグラムで視覚的にばらつきを確認し、具体例を挙げて解説（例：テスト点数の分布が偏っている場合と均等な場合）。