DIME MAGAZINE
もうすぐやってくるクリスマス。子どもの頃はサンタさんからのプレゼントを心待ちにし、12月25日まであと何日か、指折り数えていたという大人は多いに違いない。
そんなクリスマスプレゼントについて、令和の子どもたちはいったい、どんなものを欲しているのだろうか？
バンダイはこのほど、1995年から毎年実施している「クリスマスに関する調査」を3～12歳（α世代）の子どもを持つ、男女600人を対象にアンケート調査を実施。
今回は過去の調査データとの比較と、11月27日に発表した「クリスマスプレゼントに関する調査」の結果を合わせて、α世代の「クリスマスプレゼント事情」としてレポートを発表した。なお、α世代とは、2010年以降生まれの子どもを指す。
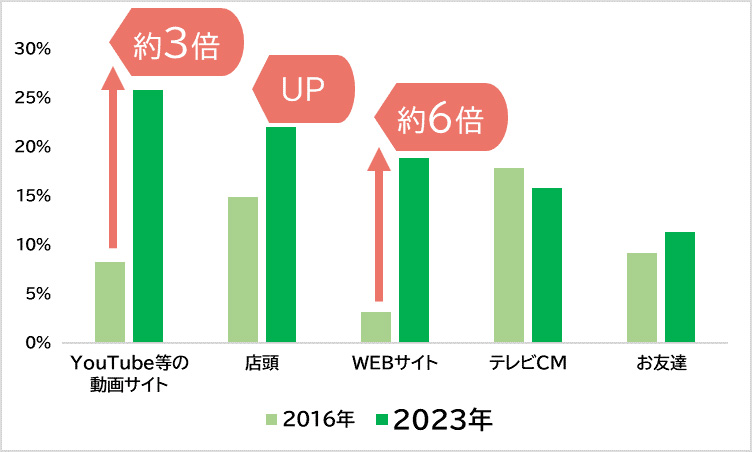
TOPIC.1：プレゼントの認知経路1位は「YouTube等の動画サイト」
α世代の欲しいクリスマスプレゼントの認知経路は、1位「YouTube等の動画サイト」、次いで2位「店頭」3位「WEBサイト（商品公式サイトなど）」となった。同様の質問を開始した2016年の結果と比較すると、「YouTube等の動画サイト」は約3倍、「WEBサイト」は約6倍になっていることから、α世代はオンラインでプレゼントを見つける子どもが増えていることがうかがえる。
一方で、「店頭」という回答も増加していることから、オンラインが主流になりつつも、実際に店頭で実物を見るという人も多いようだ。α世代は子どものころから、インターネットやSNSが当たり前に日常にあるデジタルネイティブということもあり、世代の色が反映される結果となった。
■欲しいクリスマスプレゼントの認知経路 TOP5
TOPIC.2：親がプレゼントを選ぶポイントに「知育・教育」や「オンライン機能」を重視する声が増加
α世代の子ども向けに親御さんがクリスマスプレゼントを選ぶ際に魅力を感じるポイントを聞いたところ、「知育・教育によさそう」の回答が10年前2013年当時の8%から、今回の調査では20％と約2.5倍に増加した。
理由としては、「知育要素があることで、興味関心が広がりそうだから」「小学生になったので、いろんな知識を身につけてもらいたい」などがあがった。
また、「年齢が変わっても長く楽しめそう」という回答は10年前から大きく差はないが、今回新たに「インターネットに接続・連動して楽しめそう」という点を魅力に感じるという回答がみられた。
魅力を感じる理由としては、「インターネットに接続することで、機能がアップデートされて常に飽きずに遊べそう」、「社会に出る前に予習させたい」、「これからの時代、デジタルツールを使いこなせないと生きていけないと思う」などがあがった。長く楽しんで欲しいという思いとともに、玩具を通して世の中のデジタル化に対応できる子どもになってほしいという思いが感じられる。
日本玩具協会と東京玩具人形協同組合が発表する「今年のクリスマスおもちゃ」のトレンドでも、『デジタルトイ』は今年の注目として発表された。なかでも「本物志向」「Wi-Fi」などがキーワードになっていることから、トレンドを裏付ける調査結果となった。
TOPIC.3：子どもが欲しいプレゼントに「スマートフォンなどの電子機器」が初のTOP5入り
α世代の子どもへ欲しいクリスマスプレゼントを聞くと、3年連続1位は「ゲームソフト」となった。今年は調査開始以来初めて、「スマートフォン・タブレット・PCなどの電子機器（本物）」が4位と初のTOP5入った。学校でタブレットを使う子どもが増えている影響か、「家でも使いたい」「大画面で動画を見たい」などの理由があがり、TOPIC.1同様欲しいプレゼントの内容にも世代の色が反映される結果となった。
＜調査概要＞
・調査日時：2023年11月2日（木）～11月6日（月）
・調査地域：全国
・調査方法：インターネット調査
・調査人数：3歳～12歳の子どもを持つ男女（23歳～59歳）600人
・対象者条件：対象年齢の子どもにプレゼントを購入する予定があり、プレゼントの選定に関与する予定がある親、また、子どもと一緒に回答できる方
出典元：株式会社バンダイ
構成／こじへい
プログラミング脳がぐんぐん育つ！小学生が99×99までの2桁かけ算を暗算できる算数ドリルが話題
「VUCA」というビジネス用語がある。変動性、不確実性、複雑性、曖昧性を指す英単語の頭文字をとった造語で、AIなどの社会実装によってビジネス環境が大きく変化していることを示す。この予測困難な社会の到来を見据えて2020年3月、文部科学省は学習指導要領「生きる力」を公示。これを機に、中学受験算数の難化が囁かれるようになった。
中学受験は、受験者数が増加傾向にあるなど、競争激化の渦中にあるもののひとつだ。そして高まる受験熱は、新たなトレンドを生んだ。2ケタ同士のかけ算で使える、暗算ドリルが続々登場しているのだ。そんな数ある暗算ドリルのなかで大きな話題を呼んでいるのが、小学生向けの暗算ドリル『小学生が99×99までスイスイ暗算できる最強ドリル』（小学館）だ。
『小学生が99×99までスイスイ暗算できる最強ドリル』
岩波邦明・著
定価1200円（税込み）
『小学生が99×99までスイスイ暗算できる最強ドリル』では、この本で初出となる「あゆみ算」を扱っている。
「あゆみ算」とは、最先端のAIを学ぶ現役スタンフォード生でもある岩波邦明医師が独自に考案した画期的な暗算法のこと。
東京大学医学部在学中に開発・出版し、累計発行部数66万部のベストセラーを誇る『岩波メソッド ゴースト暗算』から、およそ12年の歳月を経て開発した最新メソッドだ。
最新メソッド「あゆみ算」では、脳のワーキングメモリに着目している。計算する際に頭の中で扱う数字の数を減らすことで、2ケタ×2ケタの暗算を簡便化。筆算よりも速くかつ正確に2ケタ同士のかけ算が暗算できるだけでなく、「最短の工程で暗算できるから、誰でも簡単にマスターできる」「問題を解くたびに情報処理能力（プログラミング脳）がグングン育つ」など、さまざまなメリットがあるという。
どうして岩波医師は新たな暗算メソッドを開発したのか？ そのきっかけは、スタンフォード大の大学院コースで最先端のAIを学ぶ中で「AI開発に数学が不可欠」という確信を得たことにあると話す。
スタンフォード大学で医療用AIの開発に挑む
岩波邦明さん／医師・現役スタンフォード生。1987年生まれ。東京大学医学部卒。在学中に暗算法「岩波メソッド ゴースト暗算」を開発。著書は66万部を超えるベストセラーに。
――岩波先生は現在、スタンフォード大学でAIの勉強をしています。医師でありながらAIを学ぶ理由をお聞かせください。
2022年11月、オープンAI社が生成AIのChatGPTを公開し、世界中に衝撃を与えました。私も衝撃を受けたひとりで、大きな衝撃を受けたと同時に、生成AIの世界に興味が湧いたのです。
翌年2月頃からプログラム言語やAIの勉強を始め、現在はスタンフォード生として大学院コースを受講しています。
――最新のAIについて勉強するなかで、気づきがあったそうですね。
はい。生成AIは100％数学でできていると言っても過言ではない。そんな確信を得ました。高校数学の分野でいうと、微分や確率、ベクトルですね。数学が生成AI開発の根幹部を支えているのです。
「数学を勉強しても将来、何の役にも立たない」という言葉をよく聞きますが、数学は世界の最前線を切り開くために必須な知識だと改めて気づきました。
――「生成AIが数学でできている」とはどういうことでしょうか？
例えば、ChatGPTはどうやって回答を導き出すのでしょうか。
「今日の天気は？」という質問に、天気に対応する言葉群から答えを選んでいると考える人は多いと思いますが、実際は違います。
確かに昔はそのようなプログラムだったこともあります。しかし現在の生成AIは、数式によって確率的に最も正しい〝らしい〞ものを選んでいるのです。
開発のステージでは、この回答の精度を向上させるために、微分を用いて数十億、多いときには数千億ものパラメーターを調整しているのです。この調整によって、いわゆるAIの賢さが決まります。
――数式で導き出すということは生成AIに学習させる段階で、数字で学習させるのでしょうか？
そのとおりです。生成AIのひとつであるChatGPTは〝言語〞ではなく言語を〝数字〞に置き換えてデータを蓄積します。そのおかげで生成AIは、それぞれの言語モデルを習得させる必要がなくなります。ChatGPTが英語だけでなく日本語やほかの言語でも高い性
能を発揮できるのは、それが理由のひとつだと考えられます。
――先生はAIを勉強した先に、どのようなビジョンを思い描いているのでしょうか？
医療用の生成AIを開発したいと思っています。
例えば、医療画像を生成するAIです。X線写真を学習させた画像生成AIがあれば診療、研究、教育など多分野で活用できるようになるでしょう。自閉症の人たちをサポートする対話型AIの開発も考えています。ジョブインタビュー（就職面接）の練習やアドバイスをしてくれるAIがあれば、自閉症の方々の生活を大きく助けることができるでしょうし、そういった医師という仕事に直結する生成AIの開発ができればと、精進しています。（続く）
特別企画「ラッキーあゆみ算（1）」の解き方を動画で解説
『小学生が99×99までスイスイ暗算できる最強ドリル』（小学館）では、2ケタ同士のかけ算全8100パターンに対応する新しい暗算法「あゆみ算」ほか、6つの暗算法「ラッキーあゆみ算」を収録している。
そこで本書で紹介している「ラッキーあゆみ算」のひとつ〝11×11から19×19までの2ケタ同士のかけ算〟の暗算法をおよそ1分で解説してもらった。
最新号
